Integración Múltiple

INTEGRACIÓN MÚLTIPLE

La integración es un concepto fundamental del cálculo y del análisis matemático. Básicamente, una integral es una generalización de lasuma de infinitos sumandos, infinitamente pequeños.

El cálculo integral, encuadrado en el cálculo infinitesimal, es una rama de las matemáticas en el proceso de integración o antiderivación, es muy común en la ingeniería y en la ciencia también; se utiliza principalmente para el cálculo de áreas y volúmenes de regiones y sólidos de revolución.

Fue usado por primera vez por científicos como Arquímedes, René Descartes, Isaac Newton, Gottfried Leibniz e Isaac Barrow. Los trabajos de este último y los aportes de Newton generaron el teorema fundamental del cálculo integral, que propone que la derivación y la integración son procesos inversos.




Las integrales se pueden calcular sobre regiones diferentes de los intervalos. En general, una integral sobre un conjunto E de una función f se escribe:

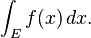
Aquí x no hace falta que sea necesariamente un número real, sino que puede ser cualquier otra cantidad apropiada, por ejemplo, unvector de R3. El teorema de Fubini demuestra que estas integrales pueden reescribirse como una integral iterada. En otras palabras, la integral se puede calcular a base de integrar las coordenadas una por una.

De la misma manera que la integral definida de una función positiva representa el área de la región encerrada entre la gráfica de la función y el eje x, la integral doble de una función positiva de dos variables representa el volumen de la región comprendida entre la superficie definida por la función y el plano que contiene su dominio. (El mismo volumen puede obtenerse a través de una integral triple— la integral de la función de tres variables — de la función constante f(x, y, z) = 1 sobre la región mencionada antes entre la superficie y el plano, lo mismo se puede hacer con una integral doble para calcular una superficie.) Si el número de variables es mayor, entonces la integral representa un hipervolumen, el volumen de un sólido de más de tres dimensiones que no se puede representar gráficamente.