Topología

Fundamentos de la Geometría

Geometría Proyectiva

¿Qué es la Geometría Proyectiva?

Es una rama de la Geometría que estudia los objetos lineales (puntos, rectas, planos, etc.) y cómo se intersectan.
Esta parte de dos principios:
ü Dos puntos definen una recta.
ü Todo par de retas se cortan en un punto (cuando son dos rectas paralelas, se dice que se cortan en un punto del infinito, un punto llamado impropio).

Realizando un recorrido histórico sabemos que la geometría tuvo sus ideas en los matemáticos griegos, pero los orígenes de la Geometría Proyectiva se da en las pinturas del Renacimiento.
Fueron los pintores renacentistas los que le dan fundamento a esta rama. Estos pintores eran arquitectos, ingenieros y os mejores matemáticos del siglo XV; como Leonardo Da Vinci, Rafael Sanzio, Alberto Durero, entre otros.
Ellos lograron plasmar en lienzos planos los objetos y las figuras tridimensionales.
La esencia de la representación tridimensional se basaba en el principio de proyección y sección. Lo que se ve de la escena depende de la posición del observador.
Imaginaron que a tela era una pantalla de cristal interpuesta entre la escena y el ojo. Para ello dedujeron Teoremas que forman parte de la Geometría Euclidea.


En el siglo XVII, se rescatan los conocimientos griegos y su aplicación de la mano de Gerard Desargues (1591-1661) quien en 1639 realizo la publicación de “Brouillon Projet” que tenía conceptos e ideas que hoy forman parte de la Geometría Proyectiva.
Los trabajos de Desargues no fueron apreciados hasta que un alumno sr, Bosse público en 1648 “El método universal de Desargues para la práctica de la perspectiva”. En dicho libro, en su apéndice escribió alunas conclusiones y el Teorema que lleva su nombre.
Este se conoce como el Teorema de Deargues y dice:
“Si dos triángulos están en perspectiva desde un punto, y sus pares de lados correspondientes se cortan, entonces los tres puntos de intersección están alineados”







Destacamos que durante los siglos XVII y XVIII la geometría proyectiva fue dejada de lado, y eso se debió a que la geometría analítica demostró ser más útil en otras ramas de las ciencias.

Pero resurge en el siglo XIX de la mano del francés Gaspard Monje (1743-1818) quien invento la Geometría Descriptiva. Este de rodeo de brillantes alumnos en la Ëcole de Polytechnique, como Carnot, Poncelet, Servois, entre otros.
Su meta fue intentar evidenciar que los métodos puramente geométricos podían lograr igual o más que los meramente algebraicos o analíticos.
Concluyendo, la Geometría Proyectiva es retomada de la Mano de Jean Víctor Poncelet (1788-1867), quien dada su estadía en una cárcel rusa reconstruyo todo lo aprendido de Carnot y Monge.
Su gran aporte fue “El Principio de Dualidad”, que consiste en que a partir de cualquier Teorema o construcción de Geometría Proyectiva podemos obtener otro, llamado Teorema Dual.
Para que sea más claro veamos lo siguiente:
I. En Geometría Proyectiva como en la Geometría Euclideana: “dos puntos cualesquiera determinan una recta”
II. Pero es verdad que en la geometría Proyectiva “dos rectas cualesquiera determinan un punto”

Geometría No Euclidiana

Geometría Diferencial

La geometría diferencial

Este es un buen momento para retomar la idea de la geometría diferencial (término usado así por primera vez por Luigi Bianchi, 1856 - 1928, en 1894), pues se trata de un marco teórico más general en el cual se integran las geometrías no euclidianas y más que eso: todas las geometrías. La geometría ya no trata de puntos o rectas del espacio, sino de lo que se llama variedades. El punto de partida puede decirse que era el trabajo realizado por Gauss en la construcción de mapas y la llamada geodesia, que apoyaría un nuevo enfoque sobre la naturaleza del espacio. Es decir:

"El problema de construir mapas planos de la superficie de la tierra fue uno de los que dio origen a la geometría diferencial, que se puede describir a grandes rasgos como la investigación de las propiedades de curvas y superficies en el entorno de un punto.'' [Bell, E.T.: Historia de las matemáticas, p. 365]

La geometría diferencial trata de las propiedades de las curvas y superficies que varían de un punto a otro, y son sujetas a variaciones (de punto en punto) donde tiene sentido la utilización de las técnicas del Cálculo. Gauss, en su Disquisitiones Generales circa Superficies Curvas (Investigaciones generales sobre superficies curvas) ofreció la nueva idea que usaría Riemann: una superficie se podía ver como un espacio en sí mismo.

Puede resultar interesante hacer aquí una digresión casi filosófica sobre la naturaleza de la geometría. Para Riemann, al igual que para Gauss, la geometría debía asociarse con la mecánica; por eso, buscó demostrar que los axiomas específicos de Euclides eran empíricos y no autoevidentes y necesarios en sí mismos sin tomar en cuenta la acción de la experiencia. Su estrategia fue buscar qué era lo realmente a priori en la geometría del espacio y estudiar sus consecuencias. Las otras propiedades del espacio no eran a priori. Con ello podría concluir que serían de naturaleza empírica. Es decir, buscar lo realmente necesario y autoevidente y, luego, hacer ver que lo que quedaba fuera tenía que ser empírico.






En su investigación, Riemann concluyó que, para estudiar el espacio, debía hacerse localmente y no como un todo: el espacio se debía analizar por pedazos. Eso implicaba, por ejemplo, que no se podía ofrecer resultados aplicables para todo el espacio. ¿ Cómo resumir la geometría diferencial? El estudio de las propiedades de las curvas y superficies en el espacio en una variedad diferencial, que es uno de esos pedazos a estudio. Las variedades eran el concepto más general y éstas poseían un conjunto de propiedades aplicables a cualquier variedad. Este conjunto era el de las propiedades necesarias y autoevidentes que Riemann quería encontrar. Se trataba de una geometría con n dimensiones, y donde había ciertas reglas. El espacio "normal'' tenía 3. Riemann consideró la distancia entre 2 puntos infinitamente próximos: en un espacio euclidiano, la métrica viene dada por la expresión





Si la métrica es diferente, el espacio es otro. Por ejemplo, si la métrica es:





se tiene lo que se llama un "espacio de Riemann''. Se puede establecer el espacio euclidiano (localmente, porque en Riemann todo es por pedazos), como un caso particular de un espacio deRiemann.

La teoría de geometrías de más de 3 dimensiones había sido desarrollada por el matemático alemán Hermann Grassmann en una obra de 1844: Ausdehnungslehre. Sus trabajos abrieron el camino al análisis vectorial para espacios afines y métricos. También Cayley había usado el concepto de espacio de n dimensiones, y Plücker también hizo contribuciones. Tomaría más tiempo, sin embargo, para que se le diera plena importancia a este tipo de espacios en la comunidad de matemáticos.

Para Riemann el espacio físico era un caso específico de una variedad diferencial. Por lo tanto, la geometría del espacio no podría ser deducida del conjunto de propiedades generales de las variedades. ¿Cómo obtener entonces las propiedades que distinguen el espacio físico de otras variedades de tres dimensiones? Respuesta: por medio de la experiencia. Es la experiencia la que debe decidir si las propiedades específicas que sintetiza la geometría euclidiana corresponden a la realidad o no. Las implicaciones filosóficas y científicas son aquí muchas. Por ejemplo, los axiomas de la geometría euclidiana podrían corresponder o no con el mundo circundante. Pero, ¿quién lo debe determinar? No la geometría, sino la física.

¿Más consecuencias? Sin duda. Aquí se introducía una visión del espacio radicalmente diferente de la que incluso hoy en día nos resulta normal. Vamos a usar un listado de propiedades del espacio físico dadas por el matemático inglés William K. Clifford para contribuir a entender aun más lo que suponía esta aproximación en la geometría:

"Riemann ha demostrado que existen diferentes clases de líneas y superficies, de la misma manera que existen diferentes clases de espacios de tres dimensiones y que sólo podemos averiguar por la experiencia a cuál de estas clases pertenece el espacio en que vivimos. En particular, los axiomas de la geometría plana son ciertos dentro de los límites de experimentación en la superficie de una hoja de papel y, sin embargo, sabemos que la hoja está realmente cubierta de un cierto número de lomas y surcos, sobre los que (al no ser cero la curvatura total) estos axiomas no son ciertos. De manera análoga, dice que aunque los axiomas de la geometría del sólido son ciertos dentro de los límites de experimentación para porciones finitas de nuestro espacio, todavía no tenemos motivo para concluir que son ciertos para porciones muy pequeñas; y si por ello puede obtenerse alguna explicación de los fenómenos físicos, tendremos razones para concluir que ellos no son ciertos para regiones muy pequeñas del espacio.

Deseo indicar aquí un método por el cual estas especulaciones pueden aplicarse a la investigación de los fenómenos físicos. Mantengo, en efecto:

(1) Que, de hecho, las porciones pequeñas del espacio son de naturaleza análoga a las pequeñas colinas de una superficie que en promedio es plana; es decir, que las leyes ordinarias de la geometría no son válidas en ellas.

(2) Que esta propiedad de curvatura o torsión está pasando continuamente de una porción a otra del espacio en forma de onda.

(3) Que esta variación de la curvatura del espacio es lo que realmente sucede en los fenómenos que llamamos movimiento de materia, ya sean ponderables o etéreos.

(4) Que en el mundo físico no sucede otra cosa que esta variación, sujeta (posiblemente) a la ley de continuidad. Estoy intentando un método general para explicar las leyes de doble refracción a partir de estas hipótesis, pero no he llegado a ningún resultado suficientemente decisivo para comunicarlo. [Clifford, William Kingdon: "Teoría de la materia en el espacio'', p. 159]

En este espacio la curvatura varía de lugar en lugar y, además, debido al movimiento de la materia, la curvatura cambia también de tiempo en tiempo.

¿Conclusión? Hay variación debida al espacio y al tiempo. Entonces: es imposible que las leyes de la geometría euclidiana se puedan aplicar en un espacio de este tipo. Una asociación entre espacio y materia, como ésta que se encuentra en las conclusiones de Clifford y Riemann, empujó en la dirección de la teoría de la relatividad

Probailidad y Estadística

Probabilidad y estadística from Alejandra Agreman

Análisis Vectorial

Matrices

Álgebra Simbólica

Álgebra Moderna

Los aportes del álgebra (1) from huachuney

Teoría de Números

TEORÍA DE NÚMEROS

“Gauss es uno de los más importantes matemáticos de la historia. Los diarios de su juventud muestran que ya en sus primeros años había realizado grandes descubrimientos en teoría de números, un área en la que su libro Disquisitiones arithmeticae (1801) marca el comienzo de la era moderna. 

En su tesis doctoral presentó la primera demostración apropiada del teorema fundamental del álgebra. A menudo combinó investigaciones científicas y matemáticas. Por ejemplo, desarrolló métodos estadísticos al mismo tiempo que investigaba la órbita de un planetoide recién descubierto, realizaba trabajos en teoría de potencias junto a estudios del magnetismo, o estudiaba la geometría de superficies curvas a la vez que desarrollaba sus investigaciones topográficas.

De mayor importancia para el álgebra que la demostración del teorema fundamental por Gauss fue la transformación que ésta sufrió durante el siglo XIX para pasar del mero estudio de los polinomios al estudio de la estructura de sistemas algebraicos. Un paso importante en esa dirección fue la invención del álgebra simbólica por el inglés George Peacock. Otro avance destacado fue el descubrimiento de sistemas algebraicos que tienen muchas propiedades de los números reales. 

Entre estos sistemas se encuentran las cuaternas del matemático irlandésWilliam Rowan Hamilton, el análisis vectorial del matemático y físico estadounidense Josiah Willard Gibbs y los espacios ordenados de n dimensiones del matemático alemán Hermann Günther Grassmann. 

Otro paso importante fue el desarrollo de la teoría de grupos, a partir de los trabajos de Lagrange. Galois utilizó estos trabajos muy a menudo para generar una teoría sobre qué polinomios pueden ser resueltos con una fórmula algebraica.

Del mismo modo que Descartes había utilizado en su momento el álgebra para estudiar la geometría, el matemático alemán Felix Klein y el noruego Marius Sophus Lie lo hicieron con el álgebra del siglo XIX. Klein la utilizó para clasificar las geometrías según sus grupos de transformaciones (el llamado Programa Erlanger), y Lie la aplicó a una teoría geométrica de ecuaciones diferenciales mediante grupos continuos de transformaciones conocidas como grupos de Lie. En el siglo XX, el álgebra se ha aplicado a una forma general de la geometría conocida como topología.

UNIDAD 6: MATEMÁTICAS DE LOS SIGLOS XIX Y XX

 MATEMÁTICAS DE LOS SIGLOS XIX Y XX

Probabilidad

PROBABILIDAD DEL SIGLO XVIII

Durante el siglo XVIII, debido muy particularmente a la popularidad de los juegos de azar, el cálculo de probabilidades tuvo un notable desarrollo sobre la base de la anterior definición de probabilidad. 

Destacan en 1713 el teorema de Bernoulli y la distribución binomial, y en 1738 el primer caso particular estudiado por De Moivre » , del teorema central del límite. En 1809 Gauss » inició el estudio de la teoría de errores y en 1810 Laplace, que había considerado anteriormente el tema, completó el desarrollo de esta teoría. 

En 1812 Pierre Laplace » publicó Théorie analytique des probabilités en el que expone un análisis matemático sobre los juegos de azar.

Geometría

Álgebra y Teoría de Números

Fundamentos del Cáculo

FUNDAMENTOS DEL CÁLCULO

El cálculo se deriva de la antigua geometria griega. Democrito calculó el volumen de piramides y conos, se cree que considerándolos formados por un número infinito de secciones de grosor infinitesimal (infinitamente pequeño), y Eudoxo y Arquímides utilizaron el "método de agotamiento" para encontrar el área de un círculo con la exactitud requerida mediante el uso de polígonos inscritos. Sin embargo, las dificultades para trabajar con números irracionales y las paradojas de Zenon de Eleaimpidieron formular una teoría sistemática del cálculo. 

En el siglo XVII, Francesco B. Cavalieri yEvangelista Torricelli ampliaron el uso de los infinitesimales, y Descartes y Pierre de Fermat utilizaron el algebra para encontrar el área y las tangentes (integración y diferenciación en términos modernos). 

Fermat e Isaac Barrow tenían la certeza de que ambos cálculos estaban relacionados, aunque fueron Isaac Newton (hacia 1660) y Gottfried W. Leibniz (hacia 1670) quienes demostraron que son inversos, lo que se conoce como teorema fundamental del cálculo. El descubrimiento de Newton, a partir de su teoría de la gravedad, fue anterior al de Leibniz, pero el retraso en su publicación aún provoca disputas sobre quién fue el primero. Sin embargo, terminó por adoptarse la notación de Leibniz.

En el siglo XVIII aumentó considerablemente el número de aplicaciones del cálculo, pero el uso impreciso de las cantidades infinitas e infinitesimales, así como la intuición geométrica, causaban todavía confusión y controversia sobre sus fundamentos. Uno de sus críticos más notables fue el filósofo irlandés George Berkeley. En el siglo XIX los analistas matemáticos sustituyeron esas vaguedades por fundamentos sólidos basados en cantidades finitas: Bernhard Bolzano y Augustin Louis Cauchy definieron con precisión los límites y las derivadas; Cauchy y Bernhard Riemann hicieron lo propio con las integrales, y Julius Dedekind y Karl Weierstrass con los números reales. 

Por ejemplo, se supo que las funciones diferenciables son continuas y que las funciones continuas son integrables, aunque los recíprocos son falsos. En el siglo XX, el análisis no convencional, legitimó el uso de los infinitesimales. Al mismo tiempo, la aparición de los ordenadores o computadoras ha incrementado las aplicaciones del cálculo.

Cálculo

CÁLCULO SIGLO XVIII

Durante buena parte del siglo los discípulos de Newton y Leibniz se basaron en sus trabajos para resolver diversos problemas de física, astronomía e ingeniería, lo que les permitió, al mismo tiempo, crear campos nuevos dentro de las matemáticas. Así, los hermanos Bernoulli inventaron el cálculo de variaciones y el matemático francés Monge la geometría descriptiva. Lagrange, también francés, dio un tratamiento completamente analítico de la mecánica, realizó contribuciones al estudio de las ecuaciones diferenciales y la teoría de números, y desarrolló la teoría de grupos. Su contemporáneo Laplace escribió Teoría analítica de las probabilidades (1812) y el clásico Mecánica celeste (1799-1825), que le valió el sobrenombre de "el Newton francés".

Sin embargo el gran matemático del siglo fue el suizo Euler, quien aportó ideas fundamentales sobre el cálculo y otras ramas de las matemáticas y sus aplicaciones. Euler escribió textos sobre cálculo, mecánica y álgebra que se convirtieron en modelos a seguir para otros autores interesados en estas disciplinas. El éxito de Euler y de otros matemáticos para resolver problemas tanto matemáticos como físicos utilizando el cálculo sólo sirvió para acentuar la falta de un desarrollo adecuado y justificado de las ideas básicas del cálculo. La teoría de Newton se basó en la cinemática y las velocidades, la de Leibniz en los infinitésimos, y el tratamiento de Lagrange era completamente algebraico y basado en el concepto de las series infinitas. Todos estos sistemas eran inadecuados en comparación con el modelo lógico de la geometría griega, y este problema no fue resuelto hasta el siglo posterior.

A los matemáticos de fines del siglo el horizonte matemático les parecía obstruido. Se había llegado al estudio de cuestiones muy complicadas a las que nos se les conocía o veía un alcance claro. Los sabios sentían la necesidad de estudiar conceptos nuevos y hallar nuevos procedimientos.

UNIDAD 5: MATEMÁTICAS DE LOS SIGLOS XVIII

MATEMÁTICAS DE LOS SIGLOS XVIII

Probabilidad

 PROBABILIDAD SIGLO XVII

Comienza en el siglo XVII cuando Pierre Fermat » y Blaise Pascal »tratan de resolver algunos problemas relacionados con los juegos de azar. Aunque algunos marcan sus inicios cuando Cardano (jugador donde los haya) escribió sobre 1520 El Libro de los Juegos de Azar (aunque no fué publicado hasta más de un siglo después, sobre 1660) no es hasta dicha fecha que comienza a elaborarse una teoría aceptable sobre los juegos.

Christian Huygens conoció la correspondencia entre Blaise Pascal y Pierre Fermat suscitada por el caballero De Méré, se planteó el debate de determinar la probabilidad de ganar una partida, y publicó (en 1657) el primer libro sobre probabilidad: De Ratiociniis in Ludo Aleae, (Calculating in Games of Chance), un tratado sobre juegos de azar.Se aceptaba como intuitivo el concepto de equiprobabilidad, se admitía que la probabilidad de conseguir un acontecimiento fuese igual al cociente.

Ecuaciones Diferenciales

HISTORIA ECUACIONES DIFERENCIALES

La teoría de las ecuaciones diferenciales comenzó a desarrollarse a finales del siglo XVII, casi simultáneamente con la aparición del Cálculo diferencial e integral. En el momento actual, las ecuaciones diferenciales se han convertido en una herramienta poderosa para la investigación de los fenómenos naturales.

En la Mecánica, la Astronomía, la Física y la Tecnología han sido causa de enorme progreso. Del estudio de las ecuaciones diferenciales del movimiento de los cuerpos celestes dedujo Newton las leyes del movimiento planetario descubiertas empíricamente por Kepler. En 1846 Le Verrier predijo la existencia del planeta Neptuno y determinó su posición en el cielo basándose en el análisis numérico de esas mismas ecuaciones.

Nacimiento del Cálculo

NACIMIENTO DEL CÁLCULO

El Cálculo constituye una de las grandes conquistas intelectuales de la humanidad. Una vez construído, la historia de la matemática ya no fue igual: la geometría, el álgebra y la aritmética, la trigonometría, se colocaron en una nueva perspectiva teórica. Detrás de cualquier invento, descubrimiento o nueva teoría, existe, indudablemente, la evolución de ideas que hacen posible su nacimiento. Es muy interesante prestar atención en el bagaje de conocimientos que se acumula, desarrolla y evoluciona a través de los años para dar lugar, en algún momento en particular y a través de alguna persona en especial, al nacimiento de una nueva idea, de una nueva teoría, que seguramente se va a convertir en un descubrimiento importante para el estado actual de la ciencia y, por lo tanto merece el reconocimiento. 

El Cálculo cristaliza conceptos y métodos que la humanidad estuvo tratando de dominar por más de veinte siglos. Una larga lista de personas trabajaron con los métodos "infinitesimales" pero hubo que esperar hasta el siglo XVII para tener la madurez social, científica y matemática que permitiría construir el Cálculo que utilizamos en nuestros días.

Newton y Leibniz son considerados los inventores del cálculo pero representan un eslabón en una larga cadena iniciada muchos siglos antes. Fueron ellos quienes dieron a los procedimientos infinitesimales de sus antecesores inmediatos, Barrow y Fermat, la unidad algorítmica y la precisión necesaria como método novedoso y de generalidad suficiente para su desarrollo posterior. Estos desarrollos estuvieron elaborados a partir de visiones de hombres como Torricelli, Cavalieri, y Galileo; o Kepler, Valerio, y Stevin. Los alcances de las operaciones iniciales con infinitesimales que estos hombres lograron, fueron también resultado directo de las contribuciones de Oresme, Arquímedes y Eudoxo. 

Finalmente el trabajo de estos últimos estuvo inspirado por problemas matemáticos y filosóficos sugeridos por Aristóteles, Platón, Tales de Mileto, Zenón y Pitágoras. Para tener la perspectiva científica e histórica apropiada, debe reconocerse que una de las contribuciones previas decisivas fue la Geometría Analítica desarrollada independientemente por Descartes y Fermat.

El siglo XVII y la disputa por la creación del cálculo:

En sus comienzos el cálculo fue desarrollado para estudiar cuatro problemas científicos y matemáticos:

1. Encontrar la tangente a una curva en un punto.
2. Encontrar el valor máximo o mínimo de una cantidad.
3. Encontrar la longitud de una curva, el área de una región y el volumen de un sólido.
4. Dada una fórmula de la distancia recorrida por un cuerpo en cualquier tiempo conocido, encontrar la velocidad y la aceleración del cuerpo en cualquier instante. Recíprocamente, dada una fórmula en la que se especifique la aceleración o la velocidad en cualquier instante, encontrar la distancia recorrida por el cuerpo en un período de tiempo conocido.

Teoría de Ecuaciones

HISTORIA TEORÍA DE ECUACIONES

En este trabajo sobre las ecuaciones vamos a reseñar diferentes aspectos donde examinaremos estas operaciones matemáticas su sus formas más sencillas.

Es a partir de la Segunda mitad del siglo VXII y siguientes donde surge el desarrollo de esta importante disciplina de las ciencias exactas, y definimos el termino ecuación como una igualdad en la que hay una o varias cantidades desconocidas llamadas incógnitas y que solo se verifica o es verdadera para determinados valores de las incógnitas, las cuales se representan por las últimas letras del alfabeto x, y, z x u v.

Destacándose para la época los matemáticos mas importantes y sobresalientes como Isaac Newton, Galilei Galileo, Sócrates Descartes y otros más.

Por esto en este contenido del presente trabajo sobre las ecuaciones vamos a ver el término ecuación sus diferentes definiciones, clasificación, su importancia y su aplicación en la vida diaria.

El comienzo de una verdadera teoría de ecuaciones se atribuye generalmente a Viète, matemático francés de finales del siglo XVI.

Si bien todavía se niega a incorporar los avances de Bombelli —es decir, los números negativos y los números «imaginarios»—, obtiene tres resultados fundamentales que se pueden resumir en el uso de letras para representar variables y coeficientes y los sistemas de coordenadas. El resultado más celebrado es probablemente lo que él llamaba la «lógica especiosa» y que actualmente se califica de cálculo utilizando letras. Viète categorizó en dos grupos el uso de las letras en matemáticas:

En relación al álgebra, el uso de las letras se extiende y se perfecciona en Europa en el transcurso del siglo XVI, pero ya existía en la obra de Diofanto: 

una letra se suma o se multiplica y juega el papel de incógnita en una ecuación. En geometría, este uso ha sido habitual ya desde la antigüedad, una letra designa un tamaño o un objeto no especificado, un punto, una recta, una distancia entre dos puntos sobre una figura, etc. 

Los principios generales de resolución de las ecuaciones no podían ser establecidos más que con la ayuda de la geometría, como el uso de gnomones para las identidades notables, después ilustrados con ejemplos de ecuaciones polinómicas con coeficientes numéricos, que Viète consideró que pertenecían a la «lógica de los números».
Viète introduce una segunda categoría de letras para los coeficientes. 

Estos son también valores que se consideran como fijados, incluso si no se les conoce, es el que ahora se llama un parámetro. Transportando al álgebra una antigua costumbre geométrica, Viète crea la «lógica especiosa». 

Este nuevo enfoque significa considerar una ecuación como una expresión del tipo: ax2 + bx = c; de hecho, poder resolver esta ecuación es poder ser capaz de resolver todas las ecuaciones de segundo grado. Un único caso general de lógica especiosa permite tratar un sinfín de casos particulares procedentes de la lógica de los números.

Geometría

GEOMETRÍA DEL SIGLO XVII

La geometría avanzó muy poco desde el final de la era griega hasta la edad media. El siguiente paso importante en esta ciencia lo dio el filósofo y matemático francés René Descartes, cuyo tratado "El Discurso del Método", publicado en 1637, hizo época. Este trabajo fraguó una conexión entre la geometría y el álgebra al demostrar cómo aplicar los métodos de una disciplina en la otra. Éste es un fundamento de la geometría analítica, en la que las figuras se representan mediante expresiones algebraicas, sujeto subyacente en la mayor parte de la geometría moderna.

Otro desarrollo importante del siglo XVII fue la investigación de las propiedades de las figuras geométricas que no varían cuando las figuras son proyectadas de un plano a otro.

Un ejemplo sencillo de geometría proyectiva queda ilustrado en la figura 1.





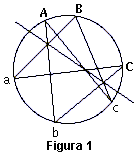
Si los puntos A, B, C y a, b, c se colocan en cualquier posición de una cónica, por ejemplo una circunferencia, y dichos puntos se unen A con b y c, B con c y a, y C con b y a, los tres puntos de las intersecciones de dichas líneas están en una recta.






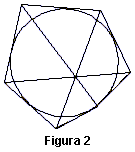
De la misma manera, si se dibujan seis tangentes cualesquiera a una cónica, como en la figura 2, y se trazan rectas que unan dos intersecciones opuestas de las tangentes, estas líneas se cortan en un punto único.






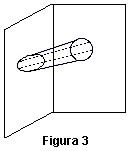
Este teorema se denomina proyectivo, pues es cierto para todas las cónicas, y éstas se pueden transformar de una a otra utilizando las proyecciones apropiadas, como en la figura 3, que muestra que la proyección de una circunferencia es una elipse en el otro plano.

Video Teoría de Números

Teoría de Números

Breve historia de la teoría de números

Prehistoria

Podemos decir que la teoría de números empezó con el matemático griego Diofanto de Alejandría en el siglo III d.c. Diofanto escribió trece libros (siete de los cuales se han perdido) dedicados a la resolución de ecuaciones algebraicas, intentando dar métodos para encontrar sus soluciones enteras o racionales. Algunos ejemplos de los problemas que trataba en su libro son: ¿Qué números son suma de dos números al cuadrado? ¿Qué números son suma de tres números al cubo?

Pero la contribución (indirecta) más importante de Diofanto fue a partir de la traducción al latín de los seis primeros libros con el nombre de Aritmética en 1621 por C.G. Bachet. Esta
traducción fue la que inspiró al verdadero padre de la teoría de números, Pierre de Fermat.

Fermat (1601-1665)

Pierre de Fermat es uno de los matemáticos más importantes de la historia. Aunque de hecho no era matemático "profesional" sino juez. Vivió durante la mayor parte de su vida en Toulouse, dedicandose en las horas libres a las matemáticas. Entre los resultados más importantes que obtuvo podemos destacar la invención (junto con Descartes) de las ahora llamadas coordenadas cartesianas, que permiten "traducir" los problemas geométricos a problemas algebraicos.

Pero los resultados que le han hecho más famoso fueron sin duda los que obtuvo trabajando inspirado en el libro de Diofanto, que dieron origen a la teoría de números. Aunque debido a
la forma de trabajar de Fermat, que no publico sus resultados en vida y solo divulgaba a
través de cartas a sus amigos y colegas, tenemos pocas indicaciones de cuales eran sus métodos para resolver los problemas.

Entre los resultados más conocidos que obtuvo (o anunció) hay:
El llamado "Pequeño teorema de Fermat": Para todo número primo p y para todo número natural a no divisible por p tenemos que p divide a ap-1-1.

El resultado más famoso de Fermat en la actualidad no es de hecho un resultado suyo, aunque se le denomina el "ultimo teorema de Fermat". 

Vídeo Geometría Analítica

Geometría Analítica

HISTORIA DE LA GEOMETRÍA ANALÍTICA

Se conoce como geometría analítica al estudio de ciertas líneas y figuras geométricas aplicando técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas.
Lo novedoso de la geometría analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x, y) = 0, donde frepresenta una función u otro tipo de expresión matemática. La idea que llevó a la geometría analítica fue: a cada punto en un plano le corresponde un par ordenado de números y a cada par ordenado de le corresponde un punto en un plano.

Fue inventada por René Descartes y por Pierre Fermat, a principios del siglo XVII, y como vimos, relaciona la matemática y el álgebra con la geometría por medio de las correspondencias anteriores.
Además, Descartes y Fermat observaron, y esto es crucial, que las ecuaciones algebraicas corresponden con figuras geométricas. Eso significa que las líneas y ciertas figuras geométricas se pueden expresar como ecuaciones y, a su vez, las ecuaciones pueden graficarse como líneas o figuras geométricas.

La idea central de toda la Geometría Analítica consiste en establecer un vínculo entre objetos geométricos y números, de tal manera que los problemas geométricos se puedan expresar de manera algebraica (analítica) y que muchos problemas algebraicos puedan encontrar una interpretación geométrica. La idea de establecer este nexo permite por un lado, representar en forma algebraica objetos puramente geométricos, con lo cual todo el arsenal de herramientas del álgebra se puede aplicar a la geometría.

Historia de los Logaritmos

Personajes importantes dentro de la historia de los logaritmos

  

El precursor de los logaritmos fue Arquímedes.

Arquímedes empezó comparando las sucesiones aritméticas con las geométricas.
La regla de Arquímedes, dice que "para multiplicar entre sí dos números cualesquiera de la sucesión de abajo, debemos sumar los dos números de la sucesión de arriba situados encima de aquellos dos. Luego debe buscarse en la misma sucesión de arriba dicha suma. El número de la sucesión inferior que le corresponda debajo será el producto deseado".




John Napier

John Napier dedujo un método sencillo para multiplicar senos de ángulos por un proceso de adición directa. Fue el inventor de la palabra logaritmo, es decir, número de razones, pues en el caso de ser el logaritmo un número entero, es el número de factores que se toman de la razón dada (base) para obtener el antilogaritmo.

Joost Bürgi

Fue un relojero y constructor de instrumentos. Se dice que concibió la idea de logaritmo antes que Napier, pero se dice que por falta de material y tiempo no lo dio a conocer.

Publico sus tablas logarítmicas en Praga, en el año 1620. Observó que las propiedades logarítmicas no se extendían solamente sobre la sucesión de potencias de base dos, sino sobre sucesiones con cualquier razón. Así nacen los logaritmos de "base vulgar" o logaritmos de Briggs. La tarea de construir la primera tabla de logaritmos en base 10 fue asumida por Briggs.



Henry Briggs

Fue profesor de geometría en Oxford. Visito a Napier en Edimburgo, y juntos llegaron a la conclusión de que el logaritmo de 1 debía ser igual a 0, mientras que el logaritmo de 10 debía ser igual a 1.

Los Logaritmos

Historia de los Logaritmos

Los orígenes del descubrimiento, o invención, de los logaritmos se remontan hasta los estudios de Arquímedes referidos a la comparación de las sucesiones aritméticas con las geométricas.

Para comprender tal comparación veamos, por ejemplo, las siguientes dos sucesiones:

1	2	3	4	5	6	7	8	9	10	11	12	13	14
2	4	8	16	32	64	128	256	512	1.024	2.048	4.096	8.192	16.384

Regularidades numéricas A los números de la sucesión primera, que es aritmética, los llamaremos logaritmos; a los de la sucesión de abajo, que es geométrica, los llamaremos antilogaritmos.

Según la regla de Arquímedes, "para multiplicar entre sí dos números cualesquiera de la sucesión de abajo, debemos sumar los dos números de la sucesión de arriba situados encima de aquellos dos. Luego debe buscarse en la misma sucesión de arriba el número correspondiente a dicha suma. El número de la sucesión inferior que le corresponda debajo será el producto deseado".

Esta comparación de dos sucesiones vuelve a aparecer en el siglo XVI en los trabajos de un matemático alemán, el suavo Miguel Stifel (1487-1567), que publicó en Nuremberg su"Arithmetica integra" en 1544. En esta obra se encuentra por primera vez el cálculo con potencias de exponente racional cualquiera y, en particular, la regla de la multiplicación:

an • am = an+m , para todo n, m racionales.

Stífel entrega también la primera tabla de sucesiones (aún no se llamaban logaritmos) que existe, aunque en forma muy rudimentaria. Contiene sólo los números enteros desde −3 hasta 6, y las correspondientes potencias de 2:

−3	−2	−1	0	1	2	3	4	5	6
1/8	1/4	1/2	1	2	4	8	16	32	64

UNIDAD 4: MATEMÁTICAS DE LOS SIGLOS XVII

MATEMÁTICAS DE LOS SIGLOS XVII

Renacimiento Matemático

Matemática en el Renacimiento

Matemática en el Renacimiento from Alejandra Agreman

UNIDAD 3: MATEMÁTICA EN EL RENACIMIENTO

 MATEMÁTICA EN EL RENACIMIENTO

Matemática en la Europa Medieval

Matemática en la Europa Medieval


El interés de los europeos medievales en las matemáticas fue impulsado por preocupaciones muy diferentes de las de los matemáticos modernos. Un elemento de conducción fue la creencia de que la matemática proporcionaba la clave para comprender el orden de la naturaleza, a menudo justificada por Platón de Timeo y el pasaje de la Biblia en el que Dios había "ordenado todas las cosas en medida, número y peso".

Temprana Edad Media

Boethius siempre tuvo un lugar para las matemáticas en el plan de estudios cuando se acuñó el término "quadrivium" para describir el estudio de la aritmética, la geometría, la astronomía, y la música. Él escribió De institutione arithmetica, una traducción libre del griego de la Introducción a la Aritmética de Nicomachus; De institutione musica, también procedente de fuentes griegas, y una serie de extractos de la Geometría de Euclides. Sus obras fueron teóricas, más que prácticas, y fueron la base del estudio matemático hasta la recuperación de las obras matemáticas griegas y árabes.


En el siglo XII, los estudiosos europeos viajaron a España y Sicilia en busca de textos científicos árabes, incluyendo el al-Jabr wa-al-Muqabilah del matemático Al-Khwarizmi, traducido al latín por Robert de Chester, y el texto completo de los Elementos de Euclides, traducidos en varias versiones por Adélard de Bath, Herman de Carintia, y Gerard de Cremona.

Estas nuevas fuentes provocaron una renovación de la matemática. Fibonacci, con el Liber Abaci, escrito en 1202 y actualizado en 1254, elaboró las primeras matemáticas significativas en Europa desde la época de Eratóstenes, un lapsus de más de un millar de años. Su trabajo introdujo la numeración arábico-hindú en Europa, y se debatieron muchos otros problemas matemáticos.

Matemática en Europa

Matemática en el Islam medieval

MATEMÁTICA EN EL ISLAM MEDIEVAL

En 642 los árabes ocuparon Alejandría, con lo que recogieron la huella de la cultura griega, para después prolongarla y perfeccionarla.
Los antecedentes de los desarrollos matemáticos que comenzaron en Bagdad alrededor del año 800 no son aún demasiado claros. Ciertamente que hubo una poderosa influencia proveniente de los matemáticos de la India, cuyo temprano desarrollo de la notación posicional y uso del cero, revistieron gran importancia. Allí comenzó un período de progreso matemático con el trabajo de al-Jwarizmi y la traducción de los textos griegos.
En 762 Al-Mansur, el décimo califa se instaló en Bagdad. Recogiendo los restos de la ciencia alejandrina, convirtió a Bagdad en una capital científica. Harún al-Rashid, quinto califa de la dinastía Abásida, comenzó su reinado el 14 de septiembre de 786. Promovió la investigación científica y la erudición. Las primeras traducciones de textos griegos al árabe, como los Elementos de Euclides por al-Hajjaj, fueron hechas durante su reinado. El séptimo califa, Abd Allah al-Ma'mun, alentó la búsqueda del conocimiento científico aún más que su padre al-Rashid, estableciendo en Bagdad una institución de investigación y traducción: la Casa de la Sabiduría (Bayt al-Hikma). Allí trabajaron al-Kindi y los tres hermanos Banu Musa, así como el famoso traductor Hunayn ibn Ishaq.En la Casa se tradujeron las obras de Euclides, Diofanto, Menelao, Arquímedes, Ptolomeo, Apolonio, Diocles, Teodosio,Hipsicles y otros clásicos de la ciencia griega. Es necesario enfatizar que estas traducciones fueron hechas por científicos, no por expertos en lenguas ignorantes de las matemáticas, y la necesidad de estas traducciones fue estimulada por las investigaciones más avanzadas de la época.

Matemática del Islam

Matemáticas de China e India

UNIDAD 2: MATEMÁTICAS EN LA EDAD MEDIA

MATEMÁTICAS EN LA EDAD MEDIA

Matemáticas Griegas

Matemática en Grecia from Alejandra Agreman

Matemáticas Griegas y Helenicas

Matemáticas China e India antigua

Matemáticas en la antigua China e India

Matemática en India

matemática de India from Alejandra Agreman

Historia Matemática en Babilonia

Números Babilónicos

Matemáticas Babilónicas

Matemáticas Babilónicas

Los babilonios vivieron en Mesopotamia, en unos claros de tierras fértiles entre los ríos Tigris y Éufrates, hacia finales del milenio IV antes de Cristo.
Desarrollaron una forma abstracta de escritura basada en símbolos cuneiformes. Sus símbolos fueron escritos en tablas de arcilla mojada cocidas al sol. Miles de estas tablillas han sobrevivido hasta nuestros días. Gracias a ello, se ha podido conocer, entre otras cosas, gran parte de las matemáticas babilónicas. El uso de una arcilla blanda condujo a la utilización de símbolos cuneiformes sin líneas curvas porque no podían ser dibujadas.

El aspecto más asombroso de las habilidades de los cálculos de los babilonios fue su construcción de tablas para ayudar a calcular.

De las tablillas babilónicas, unas 300 se relacionan con las matemáticas, unas 200 son tablas de varios tipos: de multiplicar, de recíprocos, de cuadrados, de cubos, etc.

Los problemas que se planteaban eran sobre cuentas diarias, contratos, préstamos de interés simple y compuesto.

En geometría conocían el Teorema de Pitágoras y las propiedades de los triángulos semejantes; en álgebra hay problemas de segundo , tercero e incluso de cuarto grado. También resolvían sistemas de ecuaciones.

Los babilonios fueron los pioneros en el sistema de medición del tiempo; introdujeron el sistema sexagesimal y lo hicieron dividiendo el día en 24 horas, cada hora en 60 minutos y cada minuto en 60 segundos. Esta forma de contar ha sobrevivido hasta nuestros días.

El sistema de numeración Babilónico tuvo una gran desventaja debido a la falta de un cero. Para poder interpretar números en los que se hallaba el cero, como el 3601, debía guiarse según el contexto en que éste se encontraba.

Los babilonios usaban fórmulas para hacer la multiplicación más fácil, puesto que no tenían tablas de multiplicar. Pero tenían una tabla en la que se hallaban escritos todos los cuadrados necesarios para multiplicar.
La división fue para los babilonios un proceso más difícil. No tuvieron un algoritmo para la división larga, de modo que fue necesaria una tabla de números recíprocos.

Ejercicios matemática en babilonia from Alejandra Agreman

Sistema Numérico Egipcio

Vídeo (La Matemática en Egipto)

UNIDAD 1: MATEMÁTICAS ANTIGUAS (Matemática en Egipto)

Matemática En

Egipto.

El Antiguo Egipto es la mayor civilización tecnológica de la antigüedad, el triunfo de la eficiencia y la inteligencia. Se pasa del neolítico a la historia en 2.500 años de acelerados avances técnicos. Los conocimientos científicos de los egipcios, su medicina, sus construcciones, su refinamiento siguen sorprendiendo y atrayendo.



Aquí nos vamos a ocupar de sus matemáticas. Tenían unos conocimientos matemáticos considerablemente avanzados. Sin llegar a la madurez que más adelante tendrían los griegos, los egipcios supieron solucionar los problemas que se les planteaban: tras la inundación anual del Nilo, las lindes desaparecían y tenían que volverlas a marcar, las construcciones (pirámides, templos,...), el comercio, los repartos.



El sistema de numeración egipcio, era un sistema decimal (de base 10) por yuxtaposición, así sus números se escribían de la siguiente manera:

Ejemplo: